有很多种算法可对单精度浮点数字的正弦值进行计算，但添加硬件加速器是功能最为强大的方法之一。之所以得出这一结论，是因为客户的应用要求使用此类正弦计算，而我们又针对能够提供良好、快速且高效的解决方案进行了多种方案的探索。

有很多种算法可对单精度浮点数字的正弦值进行计算，但添加硬件加速器是功能最为强大的方法之一。之所以得出这一结论，是因为客户的应用要求使用此类正弦计算，而我们又针对能够提供良好、快速且高效的解决方案进行了多种方案的探索。

为了确定哪种实现方式最适合您的应用，首先需要对代码进行分析，以查找哪种功能需要改进；其次，由于修改软件比修改硬件更简便、迅速，因而请检查是否能通过修改软件来实现您所需的高速度（有时可以）。但是如果您还需要更高的性能，那么请考虑在硬件中实现部分算法。在硬件加速的支持下，您可以轻松胜过市场上任意微控制器或DSP。

为了解该流程，让我们以现实案例为例，探讨如何开发一个需要针对单精度浮点数字进行正弦计算的军事应用。出于对高性价比的原因考虑，客户已选择了一款采用嵌入式 MicroBlaze®的Spartan®-6 FPGA 作为主系统控制器。可处理正弦计算的软件算法应运行于MicroBlaze 之上。

客户的算法主要使用浮点运算。由于算法复杂，转而采用定点运算并不妥当。此外，客户还希望避免使用定点运算时可能出现的运行过度或运行不足的情况。

客户清楚 MicroBlaze IP 可提供两种类型的浮点单元 （FPU），并已选用扩展版本（相对于基本版而言）来加速算法。但是，这样做就无法利用作为GNU工具链组成部分且随 EDK 一起交付的数学仿真库。数学库中的软件仿真例程程序运行速度非常慢，在任何情况下都应尽量避免将其用于算法中对性能起到关键作用的部分。

另外，客户还清楚 MicroBlaze FPU的两个版本都只能处理单精度数据，不能处理双精度数据。客户的算法可以明确地仅使用浮点精度数据 （float precision data）。但在开始使用数学函数时，有时也会进行隐式转换。这些转换会强制算法

在不知不觉中使用双精度数据。

步骤一：分析问题

我们的客户已经在运行他的算法，但发现该算法在MicroBlaze处理器上的运行速度偏慢。在对代码库进行特性描述后，客户发现引起速度慢的原因是正弦计算。下一步是找出其中原因并分析怎样做才能加快处理速度。

第一种方案是使用数学库提供的标准正弦函数，在客户将算法写入后，在不进行任何修改的情况下完整地运行它。主要的问题在于数学库函数仅针对双精度数据而创建，这就意味着正弦函数的原型应为如下所示：

double 九游会agsin（double angle）;

但客户希望以下列方式使用：

float sin_val;

float angle;

...

sin_val = sin（angle）;

当然，这也是可能的，而且C编译器会自动从参数角添加所需的转换，进行“双精度化”，并将函数调用的结果转回浮点值。这样通常还是由数学库函数来执行两个额外的转换函数，甚至是正弦计算。

切记，MicroBlaze的FPU为单精度版本，只能完成如下执行指令：

sin_val = （float）sin（（double）angle）;

由于数学库的正弦函数是双精度的，因而FPU无法完成正弦计算，故需要纯软件的解决方案。但缺点在于速度太慢，无法满足客户的需求。

我们验证了使用双精度数据进行正弦值的计算是执行缓慢的原因。首先我们使用下列代码，从我们的执行文件中直接创建汇编代码：

mb-objdump.exe -D executable.elf

dump.txt

检查汇编代码时，我们发现了如下代码行：

brlid r15，-15832 // 4400d300

其作用是调用数学库以进行双精度正弦计算。然后，我们测量了利用数学库函数完成单次正弦计算所需的时间，约为 38，700个CPU周期。

对于特定的任务，可以使用专用单精度函数，如计算平方根：

float sqrt_f（ float h）;

使用专用函数可以避免单、双精度函数之间的转换，而且还可充分利用MicroBlaze FPU。

但遗憾的是，在FPU上没有用于处理正弦计算的专用函数。此时，我们开始开发多个版本的算法来加速正弦值的计算，以实现更高的性能。

步骤二：创建更好的软件算法

创建硬件加速器通常需要一段时间而且也需要进行调试，因而我们试图避免在第一次运行中就采取这种方案。我们就性能问题与客户进行了沟通，获得了正弦计算的关键参数。

客户的算法要求正弦计算的参数角应具有1％的精度，而且计算出的正弦值精度应比数学库函数调用的结果高0.1%。

这些属于关键参数，而且客户告知我们，他有时必须按顺序计算多个正弦值（比如在处理之前先填入小表格）。

由于对表格的尺寸要求， 使用填充了所有数值的查找表显然不太可能。条目的最小数量为360，000个浮点数值（每个值 4 个字节）。客户想找到高速解决方案，但在大小上也应该合适。我们建议的解决方案可使用下列等式：

sin（xi） with xi = x + d

得到：

sin（x+d） = sin（x）*cos（d） +cos（x）*sin（d）

在这里，d是一个始终小于 x最小可能值（大于0）的值。这种解决方案有什么优势呢？我们需要缩小表格的大小，但会带来计算量的增加。表格从开始就划分为四个表格：

cos（x）

sin（x）

cos（d）

sin（d）

图1和图2显示了所有4个表格所需的分辨率以及这些值通常情况下的表现。这些表格仅显示了16个值的条目，用于说明需要填入我们的查找表中的值。我们在我们最终的解决方案中所使用的值要多得多。

图 1 — x 值的正弦与余弦表，范围介于0到360度之间

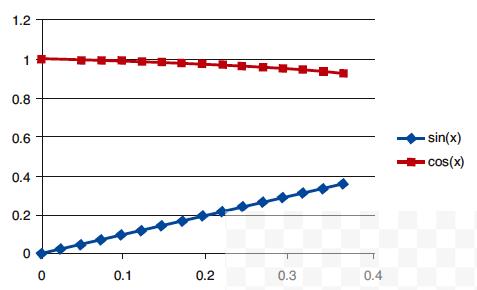
图 2 — d 值的正弦与余弦表，范围介于0到360/16度之间

实际上， 我们在每个表格中都使用了1 ， 0 2 4 个值。X的最小值为360/1024=0.3515625 度。d 的所有值都将小于等于该值。该方法可以减少存储的占用，因为完整的查找表需要 4，096个条目（每条目 4 个字节）。

使用这种方案，我们能够实现的自变量总体精度为：

360/（1024*1024） = 0，000343 degree

而且这个精度非常好。计算充分利用了MicroBlaze FPU。

真正的计算会占用一些时钟周期，具体来说，需要进行两次fmul运算和一次fadd运算。不过，我们还需要进行一些其它计算。首先，我们必须把自变量 xi拆分成两个值，对应x和d；然后，我们将这两个值从表格中读出；最后，我们必须使用新的算法才能计算结果。

我们在软件中实现算法并对其进行测试时，我们耗用的时钟周期总数为6，520个。

为了进一步提高分辨率，我们可以使用下列的象限关系：

第一象限

sin（x） = sin（x）

第二象限

sin（x） = sin（π - x）

第三象限

sin（x） = -sin（π + x）

第四象限：

sin（x） = -sin（2* π - x）

这在保持表格大小不变的同时还可将总体分辨率提高4倍。另一方面，我们需要进行更多的计算才能找出我们必须进行计算的象限是哪一个。仍然需要改进算法或缩小表格的大小（缩小四分之几）。我们还没有进行到这一步。